Reference
1. Practical Search Techniques in Path Planning for Autonomous Driving
2. Python robotics (Hybrid a star)
3. Wook's lab 블로그의 Application of hybrid A star
4. blog.Habrador.com, Explaining the Hybrid A Star pathfinding algorithm for selfdriving cars
5. Hybrid A* 原理与代码 - 知乎 (zhihu.com)
6. GitHub - zm0612/Hybrid_A_Star: Hybrid A Star algorithm C++ implementation
7. MotionPlanning/HybridAstarPlanner/hybrid_astar.py at master · zhm-real/MotionPlanning · GitHub
9. 휴리스틱 탐색 : Heuristic Search (aistudy.com)
10.Online LaTeX Equation Editor - LaTeX4technics
11.Ackerman Steering • Computer Science and Machine Learning (xarg.org)
12.블로그/웹에서 소스코드 하이라이트/구문강조 사용하기 - 개발자스럽다 (gaerae.com)
현재 진행 중인 점
1. Google Bard와 ChatGPT4.0을 이용해서 "Practical Search Techniques in Path Planning for Autonomous Driving" 논문을 한글로 번역했기 때문에 한글 번역 분이 어색하거나 틀린 곳이 많습니다. 향후, 수정할 계획 입니다.
2. 논문 중에 수식이 많은 부분은 아직 글을 옮기지 못했습니다. 향후 추가할 계획 입니다.
3. 본 논문의 알고리즘을 분석하기 위해, 참고문헌에 표기된 Hybrid A Star 소스코드를 살펴봅니다.
Abstract
We describe a practical path-planning algorithm that generates smooth paths for an autonomous vehicle operating in an unknown environment, where obstacles are detected online by the robot’s sensors. This work was motivated by and experimentally validated in the 2007 DARPA Urban Challenge, where robotic vehicles had to autonomously navigate parking lots.
(ChatGPT4.0 with Scholar AI) 이 논문에서는 미지의 환경에서 작동하는 자율주행 차량을 위한 실용적인 경로 계획 알고리즘을 제시합니다. 이 알고리즘은 차량의 센서로 실시간으로 장애물을 감지하면서 차량에 대한 부드러운 경로를 생성합니다. 이 알고리즘은 2007년 DARPA Urban Challenge에서 검증되었으며, 이 대회에서 로봇 차량들은 주차장을 자율적으로 이동해야 했습니다.
Our approach has two main steps. The first step uses a variant of the well-known A* search algorithm, applied to the 3D kinematic state space of the vehicle, but with a modified state-update rule that captures the continuous state of the vehicle in the discrete nodes of A* (thus guaranteeing kinematic feasibility of the path). The second step then improves the quality of the solution via numeric non-linear optimization, leading to a local (and frequently global) optimum.
(ChatGPT4.0 with Scholar AI) 우리의 접근법은 두 단계로 이루어집니다. 첫 번째 단계에서는 잘 알려진 A* 검색 알고리즘의 변형을 차량의 3D 운동 상태 공간에 적용합니다. 그러나 상태 업데이트 규칙은 A*의 이산 노드에서 차량의 연속 상태를 포착하도록 수정되어 경로의 운동 가능성을 보장합니다. 두 번째 단계에서는 숫자 비선형 최적화를 통해 솔루션의 품질을 향상시키며, 이로 인해 지역적(그리고 종종 전역적) 최적점에 도달합니다.
The path-planning algorithm described in this paper was used by the Stanford Racing Teams robot, Junior, in the Urban Challenge. Junior demonstrated flawless performance in complex general path-planning tasks such as navigating parking lots and executing U-turns on blocked roads, with typical fullcycle replaning times of 50–300ms.
(ChatGPT4.0 with Scholar AI) 이 알고리즘은 Urban Challenge에서 Stanford Racing Team의 로봇, Junior에 의해 사용되었습니다. Junior는 주차장을 이동하는 등의 복잡한 일반 경로 계획 작업에서 완벽한 성능을 보였으며, 전체 재계획 주기의 전형적인 실행 시간은 50-300ms였습니다."
Introduction and Related Work
We address the problem of path planning for an autonomous vehicle operating in an unknown environment. We assume the robot has adequate sensing and localization capability and must replan online while incrementally building an obstacle map. This scenario was motivated, in part, by the DARPA Urban Challenge, in which vehicles had to freely navigate parking lots. The path-planning algorithm described below was used by the Stanford Racing Team’s robot, Junior in the Urban Challenge (DARPA 2007). Junior (Figure 1) demonstrated flawless performance in complex general path-planning tasks—many involving driving in reverse—such as navigating parking lots, executing Uturns, and dealing with blocked roads and intersections with typical full-cycle replanning times of 50–300ms on a modern PC.
(ChatGPT4.0 with Scholar AI) "우리는 미지의 환경에서 작동하는 자율주행 차량을 위한 경로 계획 문제를 다룹니다. 우리는 로봇이 적절한 센싱과 위치 파악 능력을 가지고 있으며, 장애물 맵을 점진적으로 구축하면서 실시간으로 재계획을 해야 한다고 가정합니다. 이 시나리오는 부분적으로 DARPA Urban Challenge에 의해 동기를 부여받았으며, 이 도전에서 차량들은 주차장을 자유롭게 이동해야 했습니다. 아래에서 설명하는 경로 계획 알고리즘은 Stanford Racing Team의 로봇, Junior가 Urban Challenge에서 사용했습니다. Junior는 주차장을 이동하는 등의 복잡한 일반 경로 계획 작업에서 완벽한 성능을 보였으며, 많은 작업이 후진 운전을 포함하였습니다. 예를 들어 주차장을 이동하거나, U턴을 실행하거나, 막힌 도로와 교차로를 다루는 등의 작업이 있었습니다. 현대 PC에서 전체 재계획 주기의 전형적인 실행 시간은 50-300ms였습니다."
 |
| 출처: Practical Search Techniques in Path Planning for Autonomous Driving |
One of the main challenges in developing a practical path planner for free navigation zones arises from the fact that the space of all robot controls—and hence trajectories—is continuous, leading to a complex continuous-variable optimization landscape. Much of prior work on search algorithms for path planning (Ersson and Hu 2001; Koenig and Likhachev 2002; Ferguson and Stentz 2005; Nash et al. 2007) yields fast algorithms for discrete state spaces, but those algorithms tend to produce paths that are non-smooth and do not generally satisfy the non-holonomic constraints of the vehicle. An alternative approach that guarantees kinematic feasibility is forward search in continuous coordinates, e.g., using rapidly exploring random trees (RRTs) (Kavraki et al. 1996; LaValle 1998; Plaku, Kavraki, and Vardi 2007). The key to making such continuous search algorithms practical for online implementations lies in an efficient guiding heuristic. Another approach is to directly formulate the path-planning problem as a non-linear optimization problem in the space of controls or parametrized curves (Cremean et al. 2006), but in practice guaranteeing fast convergence of such programs is difficult due to local minima.
(ChatGPT4.0 with Scholar AI) 자율주행을 위한 실용적인 경로 계획 알고리즘을 개발하기 위한 주요 도전 과제 중 하나는 모든 로봇 제어의 공간이 연속적이라는 사실에서 비롯됩니다. 이는 복잡한 연속 변수 최적화 풍경을 만들어냅니다. 경로 계획을 위한 검색 알고리즘에 대한 이전의 많은 연구들(Ersson and Hu 2001; Koenig and Likhachev 2002; Ferguson and Stentz 2005; Nash et al. 2007)은 이산 상태 공간에 대한 빠른 알고리즘을 제공하지만, 이러한 알고리즘들은 대체로 부드럽지 않은 경로를 생성하며, 일반적으로 차량의 논홀로노믹 제약조건을 만족시키지 못합니다. 운동 가능성을 보장하는 대안적인 접근법은 연속 좌표에서의 전진 검색입니다. 예를 들어, 빠르게 탐색하는 무작위 트리(RRTs)를 사용합니다(Kavraki et al. 1996; LaValle 1998; Plaku, Kavraki, and Vardi 2007). 이러한 연속 검색 알고리즘을 온라인 구현에 실용적으로 만드는 핵심은 효율적인 가이드 휴리스틱에 있습니다. 또 다른 접근법은 경로 계획 문제를 제어 또는 매개변수화된 곡선의 공간에서 비선형 최적화 문제로 직접 수식화하는 것입니다(Cremean et al. 2006), 하지만 실제로는 이러한 프로그램의 빠른 수렴을 보장하는 것이 지역 최소값 때문에 어렵습니다.
Our algorithm builds on the existing work discussed above, and consists of two main phases. The first step uses a heuristic search in continuous coordinates that guarantees kinematic feasibility of computed trajectories. While lacking theoretical optimality guarantees, in practice this first step typically produces a trajectory that lies in a neighborhood of the global optimum.
(ChatGPT4.0 with Scholar AI) 우리의 알고리즘은 위에서 논의한 기존 연구를 기반으로 하며, 두 가지 주요 단계로 구성됩니다. 첫 번째 단계는 연속 좌표에서 휴리스틱 검색을 사용하여 계산된 궤적의 운동 가능성을 보장합니다. 이론적인 최적성 보장이 부족하지만, 실제로 이 첫 번째 단계는 일반적으로 전역 최적점 근처의 궤적을 생성합니다. 두 번째 단계는 conjugate gradient (CG) descent을 사용하여 해결책의 품질을 지역적으로 개선하며, 적어도 지역적으로 최적의 경로를 생성하지만, 대개 전역 최적점도 달성합니다.
The second step uses conjugate gradient (CG) descent to locally improve the quality of the solution, producing a path that is at least locally optimal, but usually attains the global optimum as well. Another practical challenge is the design of a cost function over paths that yields the desired driving behavior. The difficulty stems from the fact that we would like to obtain paths that are near-optimal in length, but at the same time are smooth and keep a comfortable distance to obstacles. A common way of penalizing proximity to obstacles is to use a potential field (Andrews and Hogan 1983; Khatib 1986; Pavlov and Voronin 1984; Miyazaki and Arimoto 1985).
(ChatGPT4.0 with Scholar AI) 또 다른 실용적인 도전 과제는 원하는 운전 행동을 산출하는 경로에 대한 비용 함수의 설계입니다. 이 어려움은 우리가 길이에서 거의 최적의 경로를 얻고 싶지만, 동시에 부드럽고 장애물로부터 안정적인 거리를 유지하고 싶다는 사실에서 비롯됩니다. 장애물에 가까움을 처벌하는 일반적인 방법은 potential field를 사용하는 것입니다(Andrews and Hogan 1983; Khatib 1986; Pavlov and Voronin 1984; Miyazaki and Arimoto 1985).
However, as has been observed by many researchers (Tilove 1990; Koren and Borenstein 1991), one of the drawbacks of potential fields is that they create high-potential areas in narrow passages, thereby making those passages effectively untraversable. To address this issues, we introduce a potential that rescales the field based on the geometry of the workspace, allowing precise navigation in narrow passages while also effectively pushing the robot away from obstacles in wider-open areas.
(ChatGPT4.0 with Scholar AI) 그러나 많은 연구자들이 관찰한 바와 같이(Tilove 1990; Koren and Borenstein 1991), potential field의 단점 중 하나는 그들이 좁은 통로에서 높은 잠재력 영역을 생성함으로써 그 통로를 실질적으로 통과할 수 없게 만든다는 것입니다. 이 문제를 해결하기 위해, 우리는 작업 공간의 기하학에 기반하여 필드를 재조정하는 잠재력을 도입하여, 좁은 통로에서 정확한 내비게이션을 가능하게 하면서도 로봇을 넓은 영역의 장애물로부터 효과적으로 밀어내게 합니다."
(코드 설명) PythonRobotics의 Hybrid A Star의 소스코드를 살펴보면서 앞으로 전개될 이론을 소스코드와 함께 분석 합니다. 우선 알고리즘 구현에 앞서, 후륜 축에 제어 중심을 갖는 자동차를 정의합니다. 이 자동차는 Ackermann steering 으로 자동차를 조향 합니다. 하지만, 자동차의 움직임을 시뮬레이션에서 단순하게 표현하기 위해 자전거 모델로 자동차를 간단하게 표현 합니다.
def pi_2_pi(angle):
return (angle + pi) % (2 * pi) - pi
def move(x, y, yaw, distance, steer, L=WB):
x += distance * cos(yaw)
y += distance * sin(yaw)
yaw += pi_2_pi(distance * tan(steer) / L) # distance/2
return x, y, yaw
(코드 설명) 자동차를 표현하는 파라미터들은 아래와 같이 정의 됩니다.
import sys import pathlib root_dir = pathlib.Path(__file__).parent.parent.parent sys.path.append(str(root_dir)) from math import cos, sin, tan, pi import matplotlib.pyplot as plt import numpy as np from utils.angle import rot_mat_2d WB = 3.0 # rear to front wheel W = 2.0 # width of car LF = 3.3 # distance from rear to vehicle front end LB = 1.0 # distance from rear to vehicle back end MAX_STEER = 0.6 # [rad] maximum steering angle BUBBLE_DIST = (LF - LB) / 2.0 # distance from rear to center of vehicle. BUBBLE_R = np.hypot((LF + LB) / 2.0, W / 2.0) # bubble radius # vehicle rectangle vertices VRX = [LF, LF, -LB, -LB, LF] VRY = [W / 2, -W / 2, -W / 2, W / 2, W / 2]
(코드 설명) BUBBLE_DIST와 BUBBLE_R을 이용해서 생성된 원은, 차량의 중심이 원점, 원점으로부터 차량의 코너점까지의 거리가 반지름 입니다.
def plot_arrow(x, y, yaw, length=1.0, width=0.5, fc="r", ec="k"):
"""Plot arrow."""
if not isinstance(x, float):
for (i_x, i_y, i_yaw) in zip(x, y, yaw):
plot_arrow(i_x, i_y, i_yaw)
else:
plt.arrow(x, y, length * cos(yaw), length * sin(yaw),
fc=fc, ec=ec, head_width=width, head_length=width, alpha=0.4)
def plot_car(x, y, yaw):
car_color = '-k'
c, s = cos(yaw), sin(yaw)
rot = rot_mat_2d(-yaw)
car_outline_x, car_outline_y = [], []
for rx, ry in zip(VRX, VRY):
converted_xy = np.stack([rx, ry]).T @ rot
car_outline_x.append(converted_xy[0]+x)
car_outline_y.append(converted_xy[1]+y)
arrow_x, arrow_y, arrow_yaw = c * 1.5 + x, s * 1.5 + y, yaw
plot_arrow(arrow_x, arrow_y, arrow_yaw)
plt.plot(car_outline_x, car_outline_y, car_color)
def plot_cllision_model(x, y, yaw):
plot_car(x, y, yaw)
plt.plot(x,y,marker='o',color='r')
cx = x + BUBBLE_DIST * cos(yaw)
cy = y + BUBBLE_DIST * sin(yaw)
circle1 = plt.Circle((cx, cy), BUBBLE_R, color='r', fill=False)
plt.gcf().gca().add_artist(circle1)
def main():
x, y, yaw = 0., 0., 1.
plt.axis('equal')
#plot_car(x, y, yaw)
plot_cllision_model(x, y, yaw)
plt.show()
(코드 설명) 아래의 그림은 시뮬레이션 차량의 충돌 모델을 표현한 결과 입니다.
def check_car_collision(x_list, y_list, yaw_list, ox, oy, kd_tree):
for i_x, i_y, i_yaw in zip(x_list, y_list, yaw_list):
cx = i_x + BUBBLE_DIST * cos(i_yaw)
cy = i_y + BUBBLE_DIST * sin(i_yaw)
ids = kd_tree.query_ball_point([cx, cy], BUBBLE_R)
if not ids:
continue
if not rectangle_check(i_x, i_y, i_yaw,
[ox[i] for i in ids], [oy[i] for i in ids]):
return False # collision
return True # no collision
def rectangle_check(x, y, yaw, ox, oy):
# transform obstacles to base link frame
rot = rot_mat_2d(yaw)
for iox, ioy in zip(ox, oy):
tx = iox - x
ty = ioy - y
converted_xy = np.stack([tx, ty]).T @ rot
rx, ry = converted_xy[0], converted_xy[1]
if not (rx > LF or rx < -LB or ry > W / 2.0 or ry < -W / 2.0):
return False # no collision
return True # collision
(코드 설명) 이제 우리는 기본적인 차량 및 충돌 모델을 정의하고, 충돌 여부를 체크하는 함수에 대하여 알아보았습니다. 다음은 본격적으로 알고리즘에 대하여 알아보겠습니다.
Hybrid-State A* Search
The first phase of our approach uses a variant of the well-known A* algorithm applied to the 3D kinematic state space of the vehicle, but with a modified state-update rule that captures continuous-state data in the discrete search nodes of A*. Just as in conventional A*, the search space $ \begin{pmatrix} x, y, \theta \end{pmatrix} $ is discretized, but unlike traditional A* which only allows visiting centers of cells, our hybrid-state A* associates with each grid cell a continuous 3D state of the vehicle, as illustrated in Figure 2.
(ChatGPT4.0 with Scholar AI) 우리의 접근법의 첫 번째 단계는 잘 알려진 A* 알고리즘의 변형을 차량의 3D 운동 상태 공간에 적용하는 것이지만, A*의 이산 검색 노드에서 연속 상태 데이터를 포착하는 수정된 상태 업데이트 규칙을 사용합니다. 기존의 A*와 마찬가지로 검색 공간 $ \begin{pmatrix} x, y, \theta \end{pmatrix} $ 이 이산화되지만, 전통적인 A*가 셀의 중심만 방문하는 것과 달리, 우리의 하이브리드 상태 A는 각 그리드 셀에 차량의 연속 3D 상태를 연결합니다. 이는 그림 2에서 보여줍니다.
그림2을 보면 전통적인 A* 알고리즘의 경우 격자 지도의 중심을 기준으로 경로를 탐색하기 때문에 경로 탐색의 결과는 이산적입니다. 하지만, 하이브리드 A*의 경우 격자 지도 상에서 4방향 이웃 또는 8방향 이웃 노드 확장 방식을 이용하여 차량의 동역학에 부합하는 경로를 생성할 수 있는 장점이 있습니다.
 |
| 출처: Practical Search Techniques in Path Planning for Autonomous Driving (코드 설명) 차량이 자연스럽게 목표 경로를 추종하기 위해서는, 차량의 운동학적 제약 조건과 환경을 고려하는 KinoDynamic 경로 계획이 중요합니다. 왜 Kinodynamic 경로 계획이 중요할까요? 예를 들어 아래의 그림에서 A* 알고리즘으로 생성된 목표 경로는 차량의 운동학적 제약 조건 때문에 생성된 경로를 따라 이동할 수 없습니다. 왜냐하면, 차량의 출발 초기 포즈는 아래를 향하고 있지만, 생성된 경로는 장애물을 피해서 위쪽으로 돌아가는 경로 입니다. 이 경로는 차량의 선회 반경의 제약 때문에 차량이 추종할 수 없습니다. 하지만, 하이브리드 A* 알고리즘을 이용해 생성된 경로는 차량의 포즈(위치, 헤딩), 및 노드 확장마다 차량의 운동학적 조건(선회 반경)등을 고려하기 때문에 차량이 추종 가능 합니다. (코드 설명) PythonRobotics의 하이브리드 A* 알고리즘에서는 아래와 같이 격자지도를 구성하였습니다. |
XY_GRID_RESOLUTION = 2.0 # [m] YAW_GRID_RESOLUTION = np.deg2rad(5.0) # [rad] x_ind = round(x / XY_GRID_RESOLUTION) y_ind = round(y / XY_GRID_RESOLUTION) yaw_ind = round(yaw / YAW_GRID_RESOLUTION)
(코드 설명) 하이브리드 A* 알고리즘은 그래프 탐색 알고리즘이기 때문에 경로 탐색은 노드의 확장을 통해 이루어 집니다. 노드의 확장 방식은 차량이 등속으로 운동하고 있다고 가정하기 떄문에, 차량의 현재 포즈 $ \begin{pmatrix} x, y, \theta \end{pmatrix} $, 현재 진행 방향 (direction), 조향각 (steering) 과 같은 운동 정보를 기록해야 합니다. 또한, 최단 경로를 계산하기 위한 매개변수인 현재 노드까지의 비용 (cost) 및 부모 노드를 기록해야 합니다.
class Node:
def __init__(self, x_ind, y_ind, yaw_ind, direction,
x_list, y_list, yaw_list, directions,
steer=0.0, parent_index=None, cost=None):
self.x_index = x_ind
self.y_index = y_ind
self.yaw_index = yaw_ind
self.direction = direction
self.x_list = x_list
self.y_list = y_list
self.yaw_list = yaw_list
self.directions = directions
self.steer = steer
self.parent_index = parent_index
self.cost = cost
As noted above, our hybrid-state A* is not guaranteed to find the minimal-cost solution, due to its merging of continuous-coordinate states that occupy the same cell in the discretized space. However, the resulting path is guaranteed to be drivable (rather than being piecewise-linear as in the case of standard A*). Also, in practice, the hybrid-A* solution typically lies in the neighborhood of the global optimum, allowing us to frequently arrive at the globally optimal solution via the second phase of our algorithm (which uses gradient descent to locally improve the path, as described below).
(ChatGPT4.0 with Scholar AI) 위에서 언급했듯이, 우리의 하이브리드 상태 A*는 이산화된 공간에서 동일한 셀을 차지하는 연속 좌표 상태를 병합하기 때문에 최소 비용 해답을 찾을 것이라는 보장이 없습니다. 그러나 결과적으로 생성되는 경로는 운전 가능하다는 것이 보장됩니다(표준 A*의 경우처럼 선분형이 아님). 또한, 실제로 하이브리드 A* 솔루션은 일반적으로 전역 최적점의 이웃에 위치하므로, 우리의 알고리즘의 두 번째 단계(아래에서 설명하는 경로를 지역적으로 개선하기 위해 경사 하강법을 사용)를 통해 전역 최적 해답에 자주 도달할 수 있습니다.
The main advantage of hybrid-state A* manifests itself in maneuvers in tight spaces, where the discretization errors become critical. Our algorithm plans forward and reverse motion, with penalties for driving in reverse as well as switching the direction of motion.
Heuristics
Our search algorithm is guided by two heuristics, illustrated in Figure 3. These heuristics do not rely on any properties of hybrid-state A* and are also applicable to other search methods (e.g., discrete A*).
(ChatGPT4.0 with Scholar AI) 하이브리드 상태 A의 주요 장점은 좁은 공간에서의 기동에서 나타나며, 여기서 이산화 오차가 중요해집니다. 우리의 알고리즘은 전진 및 후진 운동을 계획하며, 후진 운전 및 운동 방향 전환에 대한 패널티를 부과합니다.
(코드 설명) 더 부드러운 경로를 따르기 위해 우리는 몇 가지 부적절한 노드 확장 방식에 벌칙 요소를 설정합니다:
SB_COST: 정방향과 역방향 운전 전환 벌칙
BACK_COST: 후진 운전 벌칙
STEER_CHANGE_COST: 이전 노드와 조향각 불일치 벌칙
NON_STRAIGHT_COST: 조향각이 0이 아닌 경우 벌칙
이외에도 다양한 벌칙 요소를 균형시키기 위해 Heuristic Cost와 Map Cost에 비율을 곱합니다. H_COST, M_COST라는 비율을 사용합니다. 예를 들어, 알고리즘의 계산 속도가 너무 느린 경우 다른 매개 변수를 변경하지 않고 H_COST를 증가시킴으로써 생성된 경로가 보다 전통적인 A* 경로에 가까워지도록 할 수 있습니다. 경로가 비뚤어진 경우 STEER_CHANGE_COST와 NON_STRAIGHT_COST를 조정할 수도 있습니다. 그러나 주의할 점은 하나의 요소의 가중치를 증가시키면 다른 요소의 가중치가 감소한다는 것입니다.
SB_COST = 100.0 # switch back penalty cost
BACK_COST = 5.0 # backward penalty cost
STEER_CHANGE_COST = 5.0 # steer angle change penalty cost
STEER_COST = 1.0 # steer angle change penalty cost
H_COST = 5.0 # Heuristic cost
def calc_next_node(current, steer, direction, config, ox, oy, kd_tree):
x, y, yaw = current.x_list[-1], current.y_list[-1], current.yaw_list[-1]
arc_l = XY_GRID_RESOLUTION * 1.5
x_list, y_list, yaw_list = [], [], []
for _ in np.arange(0, arc_l, MOTION_RESOLUTION):
x, y, yaw = move(x, y, yaw, MOTION_RESOLUTION * direction, steer)
x_list.append(x)
y_list.append(y)
yaw_list.append(yaw)
if not check_car_collision(x_list, y_list, yaw_list, ox, oy, kd_tree):
return None
d = direction == 1
x_ind = round(x / XY_GRID_RESOLUTION)
y_ind = round(y / XY_GRID_RESOLUTION)
yaw_ind = round(yaw / YAW_GRID_RESOLUTION)
added_cost = 0.0
if d != current.direction:
added_cost += SB_COST
# steer penalty
added_cost += STEER_COST * abs(steer)
# steer change penalty
added_cost += STEER_CHANGE_COST * abs(current.steer - steer)
cost = current.cost + added_cost + arc_l
node = Node(x_ind, y_ind, yaw_ind, d, x_list,
y_list, yaw_list, [d],
parent_index=calc_index(current, config),
cost=cost, steer=steer)
return node
휴리스틱
우리의 검색 알고리즘은 그림 3에서 보여지는 두 가지 휴리스틱에 의해 안내됩니다. 이 휴리스틱들은 하이브리드 상태 A의 어떤 속성에도 의존하지 않으며, 다른 검색 방법(예: 이산 A*)에도 적용 가능합니다.
 |
| 출처: Practical Search Techniques in Path Planning for Autonomous Driving |
The first heuristic—which we call “non-holonomicwithout-obstacles”—ignores obstacles but takes into account the non-holonomic nature of the car. To compute it, we assume a goal state of (xg, yg, θg) = (0, 0, 0) and compute the shortest path to the goal from every point (x, y, θ) in some discretized neighborhood of the goal, assuming complete absence of obstacles.1 Clearly, this cost is an admissible heuristic. We then use a max of the non-holonomicwithout-obstacles cost and 2D Euclidean distance as our heuristic. The effect of this heuristic is that it prunes search branches that approach the goal with the wrong headings. Notice that because this heuristic does not depend on runtime sensor information, it can be fully pre-computed offline and then simply translated and rotated to match the current goal. In our experiments in real driving scenarios, this heuristic provided close to an order-of-magnitude improvement in the number of nodes expanded over the straightforward 2D Euclidean-distance cost.
(ChatGPT4.0 with Scholar AI)첫 번째 휴리스틱인 '비홀로노믹-장애물 없음'은 장애물을 무시하지만 차량의 비홀로노믹 특성을 고려합니다. 이를 계산하기 위해, 우리는 목표 상태를 (xg, yg, θg) = (0, 0, 0)로 가정하고, 장애물이 전혀 없다고 가정하여 목표 주변의 이산화된 이웃에서 모든 점 (x, y, θ)에서 목표까지의 최단 경로를 계산합니다. 분명히, 이 비용은 허용 가능한 휴리스틱입니다. 그런 다음 우리는 비홀로노믹-장애물 없음 비용과 2D 유클리드 거리의 최대값을 휴리스틱으로 사용합니다. 이 휴리스틱의 효과는 목표에 잘못된 헤딩으로 접근하는 검색 분기를 제거하는 것입니다. 이 휴리스틱은 런타임 센서 정보에 의존하지 않기 때문에, 완전히 사전에 계산할 수 있으며, 그런 다음 현재의 목표에 맞게 단순히 변환하고 회전시킬 수 있습니다. 실제 운전 시나리오에서의 실험에서, 이 휴리스틱은 간단한 2D 유클리드 거리 비용에 비해 노드 확장 수에서 대략 10배의 향상을 제공했습니다.
The second heuristic is a dual of the first in that it ignores the non-holonomic nature of the car, but uses the obstacle map to compute the shortest distance to the goal by performing dynamic programming in 2D. The benefit of this heuristic is that it discovers all U-shaped obstacles and dead-ends in 2D and then guides the more expensive 3D search away from these areas.
Both heuristics are mathematically admissible in the A* sense, so the maximum of the two can be used.
(ChatGPT4.0 with Scholar AI)두 번째 휴리스틱은 차량의 비홀로노믹 특성을 무시하지만,장애물 맵을 사용하여 2D에서 동적 프로그래밍을 수행함으로써 목표까지의 최단 거리를 계산합니다. 이 휴리스틱의 장점은 2D에서 모든 U자형 장애물과 막다른 길을 발견하고, 그런 다음 더 비싼 3D 검색을 이러한 영역에서 멀리 유도한다는 것입니다.
두 휴리스틱 모두 A* 의미에서 수학적으로 허용 가능하므로, 두 가지 중 최대값을 사용할 수 있습니다.
(코드 설명) Hybrid A*는 차량의 운동학 모델을 사용하여 노드를 확장합니다. 노드 확장 방법은 다음 그림과 같습니다:
그러나 주의해야 할 점은 노드 확장에 사용되는 매개 변수가 최종 경로의 품질에 매우 중요한 역할을 한다는 것입니다. 먼저, 조향각 샘플링 수인 N_STEER는 한 노드가 확장될 때 계산을 수행하는 횟수를 결정합니다. 그 다음으로는 MOTION_RESOLUTION인 한 걸음의 크기입니다. MOTION_RESOLUTION은 노드 하나로 계산되지 않고, 여러 개의 MOTION_RESOLUTION 길이가 arc_l로 누적되어야 노드로서 기록됩니다. arc_l의 길이는 하나의 그리드 셀보다 약간 큽니다. 이는 두 번의 모의 경로가 동일한 그리드 셀에 떨어지는 것을 피하기 위한 것입니다. 이제 class Node의 x_list, y_list, yaw_list를 보면 두 노드 사이의 모의 경로 포인트를 기록하고, 이러한 경로 포인트를 사용하여 충돌이 발생하는지 여부를 확인합니다.
 |
| 참조: Hybrid A* 原理与代码 - 知乎 (zhihu.com) |
(코드 설명) 위 그림을 고려하면, N_STEER와 MOTION_RESOLUTION이 클수록 생성되는 경로는 더 연속적이고 작을수록 더 이산적입니다. 그러나 동시에 계산 비용도 증가합니다. 따라서 맵의 크기와 유형에 따라 매개 변수를 수정해야 합니다. 지도가 상대적으로 희소한 경우 모의 경로를 약간 덜 밀집시킬 수 있지만, 그 반대의 경우 경로가 더 밀집되기를 원합니다.
MOTION_RESOLUTION = 0.1 # [m] path interpolate resolution
N_STEER = 20 # number of steer command
def calc_motion_inputs():
for steer in np.concatenate((np.linspace(-MAX_STEER, MAX_STEER,
N_STEER), [0.0])):
for d in [1, -1]:
yield [steer, d]
def get_neighbors(current, config, ox, oy, kd_tree):
for steer, d in calc_motion_inputs():
node = calc_next_node(current, steer, d, config, ox, oy, kd_tree)
if node and verify_index(node, config):
yield node
def calc_next_node(current, steer, direction, config, ox, oy, kd_tree):
x, y, yaw = current.x_list[-1], current.y_list[-1], current.yaw_list[-1]
arc_l = XY_GRID_RESOLUTION * 1.5
x_list, y_list, yaw_list = [], [], []
for _ in np.arange(0, arc_l, MOTION_RESOLUTION):
x, y, yaw = move(x, y, yaw, MOTION_RESOLUTION * direction, steer)
x_list.append(x)
y_list.append(y)
yaw_list.append(yaw)
if not check_car_collision(x_list, y_list, yaw_list, ox, oy, kd_tree):
return None
d = direction == 1
x_ind = round(x / XY_GRID_RESOLUTION)
y_ind = round(y / XY_GRID_RESOLUTION)
yaw_ind = round(yaw / YAW_GRID_RESOLUTION)
added_cost = 0.0
if d != current.direction:
added_cost += SB_COST
# steer penalty
added_cost += STEER_COST * abs(steer)
# steer change penalty
added_cost += STEER_CHANGE_COST * abs(current.steer - steer)
cost = current.cost + added_cost + arc_l
node = Node(x_ind, y_ind, yaw_ind, d, x_list,
y_list, yaw_list, [d],
parent_index=calc_index(current, config),
cost=cost, steer=steer)
return node Analytic Expansions
The forward search described above uses a discretized space of control actions (steering). This means that the search will never reach the exact continuouscoordinate goal state (the accuracy depends on the resolution of the grid in A*). To address this precision issue, and to further improve search speed, we augment the search with analytic expansions based on the Reed-Shepp model (Reeds and Shepp 1990). In the search described above, a node in the tree is expanded by simulating a kinematic model of the car—using a particular control action—for a small period of time (corresponding to the resolution of the grid).
(ChatGPT4.0 with Scholar AI)위에서 설명한 전진 검색은 이산화된 제어 동작(조향) 공간을 사용합니다. 이는 검색이 정확한 연속 좌표 목표 상태에 도달하지 못하게 됨을 의미합니다(A의 그리드 해상도에 따라 정확도가 달라집니다). 이 정밀도 문제를 해결하고 검색 속도를 더욱 향상시키기 위해, 우리는 Reed-Shepp 모델(Reeds and Shepp 1990)을 기반으로 한 분석적 확장을 검색에 추가합니다. 위에서 설명한 검색에서, 트리의 노드는 차량의 운동 모델을 시뮬레이션함으로써 확장되며, 특정 제어 동작을 사용하여 짧은 시간 동안(A의 그리드 해상도에 해당) 확장됩니다.
In addition to children generated in such a way, for some nodes, an additional child is generated by computing an optimal Reed-and-Shepp path from the current state to the goal (assuming an obstacle-free environment). The Reed-andShepp path is then checked for collisions against the current obstacle map, and the children node is only added to the tree if the path is collision-free. For computational reasons, it is not desirable to apply the Reed-Shepp expansion to every node (especially far from the goal, where most such paths are likely to go through obstacles). In our implementation, we used a simple selection rule, where the Reed-Shepp expansion is applied to one of every N nodes, where N decreases as a function of the cost-to-goal heuristic (leading to more frequent analytic expansions as we get closer to the goal).
(ChatGPT4.0 with Scholar AI)이러한 방식으로 생성된 자식들 외에도, 일부 노드에 대해 추가적인 자식이 현재 상태에서 목표까지의 최적의 Reed-and-Shepp 경로를 계산함으로써 생성됩니다(장애물이 없는 환경을 가정). Reed-andShepp 경로는 현재의 장애물 맵에 대해 충돌 검사를 받고, 경로가 충돌이 없는 경우에만 자식 노드가 트리에 추가됩니다. 계산상의 이유로, 모든 노드에 Reed-Shepp 확장을 적용하는 것은 바람직하지 않습니다(특히 목표에서 멀리 떨어져 있을 때, 대부분의 이러한 경로는 장애물을 통과할 가능성이 높습니다). 우리의 구현에서는 간단한 선택 규칙을 사용했으며, Reed-Shepp 확장은 목표까지의 비용 휴리스틱의 함수로 감소하는 N개의 노드 중 하나에 적용되었습니다(목표에 가까워질수록 더 자주 분석적 확장이 이루어집니다).
A search tree with the Reed-Shepp expansion is shown in Figure 4. The search tree generated by the short incremental expansion of nodes is shown in the yellow-green color range, and the Reed-Shepp expansions is shown as the single purple line leading to the goal. We found that this analytic extension of the search tree leads to significant benefits in both accuracy and planning time.
(ChatGPT4.0 with Scholar AI)Reed-Shepp 확장을 가진 검색 트리는 그림 4에서 보여집니다. 노드의 짧은 증분 확장에 의해 생성된 검색 트리는 노랑-녹색 색상 범위로 표시되며, Reed-Shepp 확장은 목표로 이어지는 단일 보라색 선으로 표시됩니다. 우리는 이 검색 트리의 분석적확장이 정확도와 계획 시간 모두에서 중요한 이점을 가져다준다는 것을 발견했습니다.
 |
| 출처: Practical Search Techniques in Path Planning for Autonomous Driving |
Path-Cost Function Using the Voronoi Field
We use the following potential field, which we call the Voronoi Field, to define the trade off between path length and proximity to obstacles. The Voronoi Field is defined as follows:
(ChatGPT4.0 with Scholar AI)"우리는 경로 길이와 장애물에 대한 근접성 사이의 균형을 정의하기 위해, 우리가 보로노이 필드(Voronoi Field)라고 부르는 다음의 잠재 필드를 사용합니다. 보로노이 필드는 다음과 같이 정의됩니다:"
where dO and dV are the distances to the nearest obstacle and the edge of the Generalized Voronoi Diagram (GVD), respectively, and α > 0, dO > 0 are constants that control the falloff rate and the maximum effective range of the field. The expression in (1) is for dO ≤ dmaxO ; otherwise, ρV (x, y) = 0.
(ChatGPT4.0 with Scholar AI)dO와 dV는 각각 가장 가까운 장애물과 일반화된 보로노이 다이어그램(GVD)의 가장자리까지의 거리이며, α > 0, dO > 0은 필드의 감소율과 최대 효과 범위를 제어하는 상수입니다. 식 (1)은 dO ≤ dmaxO인 경우에 대한 것입니다. 그렇지 않으면, ρV (x, y) = 0입니다.
This potential has the following properties: i) it is zero when dO ≥ dmaxO ; ii) ρV (x, y) ∈ [0, 1] and is continuous on (x, y) since we cannot simultaneously have dO = dV =0; iii) it reaches its maximum only within obstacles. iv) it reaches its minimum only on the edges of the GVD.
(ChatGPT4.0 with Scholar AI)이 잠재력은 다음과 같은 특성을 가지고 있습니다: i) dO ≥ dmaxO일 때 0입니다; ii) ρV (x, y) ∈ [0, 1]이며, 우리는 동시에 dO = dV =0을 가질 수 없기 때문에 (x, y)에서 연속적입니다; iii) 장애물 내에서만 최대치에 도달합니다. iv) GVD의 가장자리에서만 최소치에 도달합니다.
The key advantage of the Voronoi field over a conventional potential fields is the fact that the field value is scaled in proportion to the total available clearance for navigation. As a result, even narrow openings remain navigable, which is not always the case for standard potential fields.
(ChatGPT4.0 with Scholar AI)보로노이 필드가 기존의 잠재 필드보다 가지는 주요한 장점은 필드 값이 탐색 가능한 전체 클리어런스에 비례하여 조정된다는 사실입니다. 결과적으로, 좁은 통로조차도 항상 탐색 가능하며, 이는 표준 잠재 필드에서 항상 그런 것은 아닙니다.
Figure 5 illustrates this property. Figure 5a shows the 2D projection of the Voronoi field, and Figure 5b gives the corresponding generalized Voronoi diagram. Notice that narrow passages between obstacles that are close to each other are not blocked off by the potential, and there is always a continuous ρV = 0 path between them. Compare this to a na¨ıve potential field ρ(x, y) = α(α + dO(x, y))−1 shown in Figure 5c, which has high-potential regions in narrow passages between obstacles.
(ChatGPT4.0 with Scholar AI)그림 5는 이 특성을 보여줍니다. 그림 5a는 보로노이 필드의 2D 투영을 보여주고, 그림 5b는 해당 일반화된 보로노이 다이어그램을 제공합니다. 장애물이 서로 가까운 좁은 통로가 잠재력에 의해 차단되지 않고, 항상 ρV = 0 경로가 그 사이에 있음을 주목하세요. 이를 그림 5c에 나타난 단순한 잠재 필드 ρ(x, y) = α(α + dO(x, y))−1과 비교해보세요. 이는 장애물 사이의 좁은 통로에서 높은 잠재 영역을 가지고 있습니다.
Figure 6 shows the Voronoi Field and a driven trajectory for a real parking lot. We should note that the use of Voronoi diagrams and potential fields has long been proposed in the context of robot motion planning. For example, Voronoi diagrams can be used to derive skeletonizations of the free space (Choset and Burdick 2000). However, navigating along the Voronoi graph is not possible for a non-holonomic car.
(ChatGPT4.0 with Scholar AI)그림 6은 보로노이 필드와 실제 주차장에서의 주행 궤적을 보여줍니다. 로봇 운동 계획의 맥락에서 보로노이 다이어그램과 잠재 필드의 사용이 오래 전부터 제안되었다는 점을 주목해야 합니다. 예를 들어, 보로노이 다이어그램은 자유 공간의 스켈레톤화를유도하는 데 사용될 수 있습니다(Choset and Burdick 2000). 그러나 비홀로노믹 자동차는 보로노이 그래프를 따라 탐색할 수 없습니다.
Navigation functions (Koditschek 1987; Rimon and Koditschek 1992) and Laplace potentials (Connolly, Burns, and Weiss 1990) are also similar to our Voronoi Field in that they construct potential functions free of local minima for global navigation. We do not use the Voronoi Field for global navigation. However, we observe that for workspaces with convex obstacles, the Voronoi Field can be augmented with a global attractive potential, yielding a field that has no local minima and is therefore suitable for global navigation.
(ChatGPT4.0 with Scholar AI)네비게이션 함수(Koditschek 1987; Rimon and Koditschek 1992)와 라플라스 잠재력(Connolly, Burns, and Weiss 1990)도 우리의 보로노이 필드와 유사하게, 전역 탐색을 위한 지역 최소값이 없는 잠재 함수를 구성합니다. 우리는 보로노이 필드를 전역 탐색에 사용하지 않습니다. 그러나, 볼록한 장애물이 있는 작업 공간에 대해, 보로노이 필드는 전역 매력 잠재력과 결합될 수 있으며, 이는 지역 최소값이 없는 필드를 생성하므로 전역 탐색에 적합합니다.
 |
| 출처: Practical Search Techniques in Path Planning for Autonomous Driving |
 |
| 출처: Practical Search Techniques in Path Planning for Autonomous Driving |
Local Optimization and Smoothing
The paths produced by hybrid-state A* are often still suboptimal and worthy of further improvement. Empirically, we find that such paths are drivable, but can contain unnatural swerves that require unnecessary steering. We therefore post-process the hybrid-state A* solution by applying the following two-stage optimization procedure. In the first stage, we formulate a non-linear optimization program on the coordinates of the vertices of the path that improves the length and smoothness of the solution. The second stage performs non-parametric interpolation using another iteration of conjugate gradient with higher-resolution path discretization.
(ChatGPT4.0) 하이브리드 상태 A에 의해 생성된 경로들은 종종 여전히 최적이 아니며 추가적인 개선이 필요하다는 것을 알 수 있습니다. 경험적으로, 이러한 경로들은 운전 가능하지만 불필요한 조향을 요구하는 불필요한 회피동작을 포함할 수 있다는 것을 발견했습니다. 따라서 우리는 하이브리드 상태 A 솔루션을 다음 두 단계 최적화 절차를 적용하여 후처리합니다. 첫 번째 단계에서는 경로의 정점 좌표에 대한 비선형 최적화 프로그램을 제시하여 솔루션의 길이와 부드러움을 개선합니다. 두 번째 단계는 더 높은 해상도 경로 이산화를 사용한 켤레 기울기의 또 다른 반복을 사용한 비매개변수 보간을 수행합니다. 이 최적화 과정은 A* 탐색이 생산한 초기 경로를 좀 더 효과적이고 자연스러운 운전 경로로 개선하는데 도움이 됩니다. 이는 일반적으로 차량의 운전 행동을 개선하고 필요 이상의 조향을 줄이는 데 중요한 역할을 합니다. 이렇게 함으로써, 우리는 차량이 안전하게, 효율적으로, 그리고 가능한 한 부드럽게 원하는 목표지점에 도달하도록 경로를 개선할 수 있습니다.
----------------------------------------------------------------
... 수식이 많은 곳이라 어떻게 정리를 잘 할 수 있을까??
우선 생략!!
----------------------------------------------------------------
Figure 7 shows the effect of the second optimization and smoothing step: the red line is the A* solution, and the blue line is the path obtained by CG optimization. Using the CG smoothing described above, we obtain a path that is much smoother than the A* solution, but it is still piecewise linear, with a significant distance between vertices (around 0.5m–1m in our implementation). This can lead to very abrupt steering on a physical vehicle. Therefore, we further smooth the path using interpolation between the vertices of the CG solution. Many parametric interpolation techniques are very sensitive to noise in the input and exacerbate any such noise in the output (e.g., cubic splines can lead to arbitrarily large oscillations in the output as input vertices get closer to each other). We therefore use non-parametric interpolation, where we super-sample the path by adding new vertices, and using CG to minimize curvature of the path, while holding the original vertices fixed. The result of interpolating the path in Figure 8a is shown in Figure 8b.
(ChatGPT4.0) 그림 7은 두 번째 최적화와 평활화 단계의 효과를 보여줍니다: 빨간색 선은 A* 솔루션을, 파란색 선은 CG 최적화에 의해 얻어진 경로를 나타냅니다. 위에서 설명한 CG 평활화를 사용하면, A* 솔루션보다 훨씬 부드러운 경로를 얻을 수 있지만, 여전히 구간별 선형이며, 정점 사이의 거리는 상당히 큽니다(구현에서 약 0.5m-1m). 이는 물리적 차량에서 매우 갑작스러운 조향을 초래할 수 있습니다. 따라서 우리는 CG 솔루션의 정점 사이에서 보간을 사용하여 경로를 더욱 평활화합니다. 많은 매개변수 보간 기법들은 입력의 노이즈에 매우 민감하고 출력에서 이러한 노이즈를 과장시킵니다(예를 들어, 세제곱 스플라인은 입력 정점들이 서로 가까워질수록 출력에서 임의로 큰 진동을 초래할 수 있습니다). 그래서 우리는 비매개변수 보간을 사용하며, 새로운 정점을 추가하여 경로를 초샘플링하고, 원래의 정점을 고정시킨 채로 경로의 곡률을 최소화하는 CG를 사용합니다. 그림 8a의 경로를 보간한 결과는 그림 8b에 나타나 있습니다.
 |
| 출처: Practical Search Techniques in Path Planning for Autonomous Driving |
(코드설명) 하이브리드 A* 알고리즘의 코드는 다음과 같습니다. 알고리즘은 두 개의 리스트를 갖고 있습니다. OpenList은 Cost에 따라 노드가 작은 순서로 정렬되며, 우선순위 큐를 사용하여 구성합니다. ClosedList은 새로운 노드를 탐색할 때 마다 ClosedList에 이미 존재하는지 확인하여 중복 탐색을 방지 합니다. 따라서, ClosedList를 구성하기 위해 Hash Table을 이용합니다. 알고리즘은 OpenList에서 가장 작은 cost를 가진 노드를 탐색하면서, 도착지에 도달하거나, 또는 새로운 노드가 one shot 조건을 충족할 때까지 탐색을 진행합니다.
여기서, one shot은 노드 확장 계산 비용을 줄이기 위해, Dubin path또는 Reeds-Shepp path와 같은 차량의 운동학적 제약을 고려한 경로 계획 방법을 이용하여 경로를 계획하는 방법입니다. 우리는 휴리스틱을 계산할 때 지도의 장애물을 고려하지 않기 때문에, 만약 생성한 경로가 장애물의 충돌 없이 생성이 된다면 그 경로를 직접 이용함으로써 노드 확장 비용을 줄일 수 있기 때문 입니다.
def hybrid_a_star_planning(start, goal, ox, oy, xy_resolution, yaw_resolution):
"""
start: start node
goal: goal node
ox: x position list of Obstacles [m]
oy: y position list of Obstacles [m]
xy_resolution: grid resolution [m]
yaw_resolution: yaw angle resolution [rad]
"""
start[2], goal[2] = rs.pi_2_pi(start[2]), rs.pi_2_pi(goal[2])
tox, toy = ox[:], oy[:]
obstacle_kd_tree = cKDTree(np.vstack((tox, toy)).T)
config = Config(tox, toy, xy_resolution, yaw_resolution)
start_node = Node(round(start[0] / xy_resolution),
round(start[1] / xy_resolution),
round(start[2] / yaw_resolution), True,
[start[0]], [start[1]], [start[2]], [True], cost=0)
goal_node = Node(round(goal[0] / xy_resolution),
round(goal[1] / xy_resolution),
round(goal[2] / yaw_resolution), True,
[goal[0]], [goal[1]], [goal[2]], [True])
openList, closedList = {}, {}
h_dp = calc_distance_heuristic(
goal_node.x_list[-1], goal_node.y_list[-1],
ox, oy, xy_resolution, BUBBLE_R)
pq = []
openList[calc_index(start_node, config)] = start_node
heapq.heappush(pq, (calc_cost(start_node, h_dp, config),
calc_index(start_node, config)))
final_path = None
while True:
if not openList:
print("Error: Cannot find path, No open set")
return [], [], []
cost, c_id = heapq.heappop(pq)
if c_id in openList:
current = openList.pop(c_id)
closedList[c_id] = current
else:
continue
if show_animation: # pragma: no cover
plt.plot(current.x_list[-1], current.y_list[-1], "xc")
# for stopping simulation with the esc key.
plt.gcf().canvas.mpl_connect(
'key_release_event',
lambda event: [exit(0) if event.key == 'escape' else None])
if len(closedList.keys()) % 10 == 0:
plt.pause(0.001)
is_updated, final_path = update_node_with_analytic_expansion(
current, goal_node, config, ox, oy, obstacle_kd_tree)
if is_updated:
print("path found")
break
for neighbor in get_neighbors(current, config, ox, oy,
obstacle_kd_tree):
neighbor_index = calc_index(neighbor, config)
if neighbor_index in closedList:
continue
if neighbor not in openList \
or openList[neighbor_index].cost > neighbor.cost:
heapq.heappush(
pq, (calc_cost(neighbor, h_dp, config),
neighbor_index))
openList[neighbor_index] = neighbor
path = get_final_path(closedList, final_path)
return path
Results
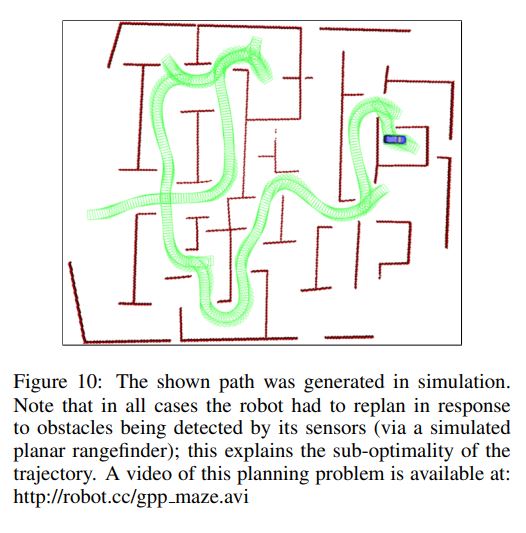
Figure 9 depicts several trajectories driven by Junior in the DARPA Urban Challenge. Figure 9a–c show U-turns on blocked roads, Figure 9d shows a task involving navigation in a parking lot. A solution to a more complex maze-like environment computed in simulation is shown in Figure 10. A video showing the robot replanning as it incrementally detects obstacles and builds an obstacle map in scenario of Figure 10 is available at http://ai.stanford.edu/ ddolgov/gpp maze.avi . We used the following parameters for our planner: the obstacle map was of size 160m×160m with 0.15cm resolution; A* used a grid of size 160m×160m×360◦ with 0.5m x-y resolution and 5◦resolution for the heading θ. Typical running times for a full replanning cycle involving the hybrid A* search, CG smoothing, and interpolation were on the order of 50–300ms.
결과
(ChatGPT4.0) 그림 9는 DARPA Urban Challenge에서 Junior가 운전한 여러 경로를 보여줍니다. 그림 9a-c는 막힌 도로에서의 U턴을 보여주며, 그림 9d는 주차장에서의 내비게이션 작업을 보여줍니다. 시뮬레이션에서 계산된 더 복잡한 미로 같은 환경에 대한 솔루션은 그림 10에 나타나 있습니다. 그림 10의 시나리오에서 로봇이 점진적으로 장애물을 감지하고 장애물 지도를 작성하면서 재계획하는 모습을 보여주는 동영상은 http://ai.stanford.edu/ ddolgov/gpp maze.avi에서 볼 수 있습니다. 우리는 계획자에 대해 다음과 같은 매개변수를 사용했습니다: 장애물 지도의 크기는 160m×160m이며 해상도는 0.15cm였습니다; A는 160m×160m×360◦의 그리드를 사용하였으며, x-y 해상도는 0.5m이고 향하는 방향 θ에 대한 해상도는 5◦였습니다. 하이브리드 A 검색, CG 평활화, 보간을 포함하는 전체 재계획 주기의 일반적인 실행 시간은 약 50-300ms의 수준이었습니다.
 |
| 출처: Practical Search Techniques in Path Planning for Autonomous Driving |
 |
| 출처: Practical Search Techniques in Path Planning for Autonomous Driving |
용어 설명
1) 휴리스틱
(ChatGPT4.0 with Scholar AI) "경로 계획(Path Planning)에서 휴리스틱(Heuristic)은 경로를 찾는 데 도움이 되는 방법이나 규칙을 의미합니다. 휴리스틱은 문제를 더 빠르게 해결하기 위해 사용되며, 최적의 해답을 찾는 것을 보장하지는 않지만, 대부분의 경우에는 충분히 좋은 해답을 제공합니다. 예를 들어, A* 검색 알고리즘에서 휴리스틱 함수는 현재 노드에서 목표 노드까지의 예상 비용을 추정하는 데 사용됩니다. 이 휴리스틱 함수는 검색을 목표 노드 방향으로 안내하여 검색 공간을 줄이고, 알고리즘의 실행 시간을 단축시킵니다. 따라서, 경로 계획에서 휴리스틱은 일반적으로 경로를 찾는 데 도움이 되는 어떤 방법이나 규칙을 의미하며, 이는 검색 공간을 줄이고, 계산 비용을 줄이며, 더 빠른 해결책을 찾는 데 도움이 됩니다."
2) Analytic Expansions
(ChatGPT4.0 with Scholar AI)"경로 계획(Path Planning)에서 사용되는 기법 중 하나로, 특정 모델을 기반으로 한 분석적인 경로 확장을 의미합니다. 이 기법은 검색 공간을 더욱 효율적으로 탐색하고, 더 정확하고 빠른 경로를 찾는 데 도움이 됩니다. "Practical Search Techniques in Path Planning for Autonomous Driving" 논문에서는 Reed-Shepp 모델을 기반으로 한 분석적 확장을 사용합니다. 이 모델은 차량의 특정 제어 동작(예: 전진, 후진, 회전 등)에 대한 최적의 경로를 계산하는 데 사용됩니다. 이 확장은 장애물이 없는 환경에서 현재 상태에서 목표 상태까지의 최적의 Reed-Shepp 경로를 계산하는 것을 포함합니다. 이렇게 계산된 경로는 현재의 장애물 맵에 대해 충돌 검사를 받고, 경로가 충돌이 없는 경우에만 검색 트리에 추가됩니다. 이렇게 하면 검색 공간을 더욱 효율적으로 탐색할 수 있으며, 더 정확하고 빠른 경로를 찾는 데 도움이 됩니다. 이러한 분석적 확장은 검색 트리의 정확도를 향상시키고 계획 시간을 줄이는 데 중요한 이점을 제공합니다."
コメント
コメントを投稿